ЛЕКЦИЯ
5
3. ВЕКТОРНАЯ АЛГЕБРА
3.1. Понятие вектора
О п р е д е л е н и е. Вектором
(геометрическим вектором) называется направленный отрезок. Обозначается
символами ![]() . Вектор имеет длину
. Вектор имеет длину ![]() , направление – угол
между вектором и горизонтальной осью. Нулевой вектор – вектор, длина которого
равна нулю.
, направление – угол
между вектором и горизонтальной осью. Нулевой вектор – вектор, длина которого
равна нулю.
О п р е д е л е н и е. Коллинеарными
называются векторы, лежащие на одной прямой или на параллельных прямых
(направления могут совпадать или быть противоположными).
![]()
![]() сонаправленные
сонаправленные
![]()
![]()
![]()
![]() Противоположно направленные
Противоположно направленные
![]()
![]()
![]()
![]()
О п р е д е л е н и е. Компланарными
называются три вектора, лежащие на
одной плоскости или на параллельных плоскостях.
Существуют
следующие типы векторов
1.
свободные векторы
(перемещаются в любом направлении),
2.
скользящие векторы
(перемещаются по прямой),
3.
связанные векторы
(начало или конец вектора зафиксированы).
Два вектора называются равными, если они имеют
одинаковую длину и одно направление.
3.2 Линейные операции над векторами
О п р е д е л е н и е. Суммой векторов ![]() и
и ![]() называется вектор
называется вектор ![]() , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора ![]() , а конец с вектором
, а конец с вектором ![]() , при условии, что конец вектора
, при условии, что конец вектора ![]() совпадает с началом
вектора
совпадает с началом
вектора ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Операция
сложения векторов обладает теми же свойствами, что и операция сложения для
вещественных чисел.
Разность
векторов – обратная операция сложению векторов. Вектор ![]() называется разностью
векторов
называется разностью
векторов ![]() и
и ![]() , если
, если ![]() . Обозначается
. Обозначается ![]() .
.
О п ре д е л е н и е. Произведением вектора ![]() на число
на число ![]()
![]() называется вектор
называется вектор ![]() , длина которого равна
, длина которого равна ![]() , а направление совпадает, если
, а направление совпадает, если ![]() , противоположно, если
, противоположно, если ![]() <0.
<0.
Т е о р е м а. Если вектор ![]() коллинеарен вектору
коллинеарен вектору ![]() , не равному нулю, то существует такое число
, не равному нулю, то существует такое число ![]() , что
, что ![]() =
=![]()
![]() .
.
![]() 1)
1) ![]() >0,
>0,
![]()
![]()
![]()
![]()
![]() О А О В
О А О В
А
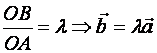
![]()
2) ![]() < 0
< 0
![]()
![]()
![]()
![]()
![]()
![]()
![]() О А
О А
В
О А
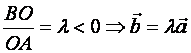 .
. ![]()
Разность
векторов можно представить в виде
![]() .
.
Операция
умножение векторов на число обладает теми же свойствами, что и произведение
вещественных чисел.
О
п р е д е л е н и е. Система
векторов ![]() называется линейно
зависимой, если существует такие неравные одновременно нулю числа
называется линейно
зависимой, если существует такие неравные одновременно нулю числа ![]() ,что
,что
![]() .
.
Система
векторов называется линейно независимой, если это равенство возможно только при
![]() .
.
Любые два коллинеарных вектора линейно зависимые.
Любые три компланарных вектора на плоскости линейно зависимые. Любые четыре
вектора в пространстве линейно зависимые.
Рассмотрим три компланарных
вектора ![]() .
.
1.
Совместим начала
этих векторов с точкой О.
D С
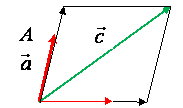
О ![]() В E
В E
2.
Проведем прямые
через эти векторы.
3.
Проведем через
точку С прямые, параллельные векторам ![]() и
и ![]()
4.
![]() ,
,
![]() .
(2)
.
(2)
Выражение
(2) можно преобразовать следующим образом
![]()
![]() .
(3)
.
(3)
Из
выражения (3) и следует, что компланарные векторы линейно зависимые.
Справедливо и обратное утверждение, что три линейно зависимых вектора
компланарны.
Выражение (2) называется разложением вектора ![]() по векторам
по векторам ![]() . Аналогично доказывается,
что любые четыре вектора в пространстве линейно зависимы.
. Аналогично доказывается,
что любые четыре вектора в пространстве линейно зависимы.
Если векторы ![]() не компланарны, т.е.
линейно независимы, то любой четвертый вектор
не компланарны, т.е.
линейно независимы, то любой четвертый вектор ![]() можно представить в виде линейной комбинации
можно представить в виде линейной комбинации
![]() .
(3)
.
(3)
Выражение (3) называется
разложением вектора ![]() по векторам
по векторам ![]() .
.
3.3 Системы координат
О п р е д е л е н и е. Базисом в
пространстве (на плоскости) называется совокупность любых трех (двух) линейно
независимых векторов. Базис обозначается
![]()
О п р е д е л е н и е. Системой
координат называется совокупность
базиса и точки О, называемой началом.

![]()
![]() О
О
![]()
![]()
Аффинная
система координат. ![]() и
и 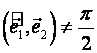 .
.
 Y
Y
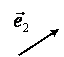
![]()
![]()
![]() О
X
О
X
Декартова
прямоугольная система координат (ДПСК).
![]() и
и 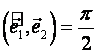 .
.
![]() Y
Y
![]()
![]()
 y
y
![]()
![]()
![]()
![]()
![]()
О x X
Всякий вектор ![]() можно представить в виде
линейной комбинации базисных векторов.
можно представить в виде
линейной комбинации базисных векторов.
![]() .
.
Числа
![]() в этом случае
называются координатами вектора
в этом случае
называются координатами вектора ![]() в базисе
в базисе ![]() . Векторы, длина которых равна 1 – единичные векторы.
Ортогональные векторы, если они взаимно перпендикулярны.
. Векторы, длина которых равна 1 – единичные векторы.
Ортогональные векторы, если они взаимно перпендикулярны.
Ортонормированный базис – это базис, состоящий из единичных взаимно
перпендикулярных векторов
![]() .
.
На
практике чаще используется ортонормированный базис ![]() ,
,
образующий
правую тройку.
Векторы ![]() образуют правую
тройку, если поворот первого из них ко второму с конца третьего вектора
проводится по часовой стрелке.
образуют правую
тройку, если поворот первого из них ко второму с конца третьего вектора
проводится по часовой стрелке.
О п р е д е л е н и е. Проекцией вектора ![]() на вектор
на вектор ![]() или на ось и называется число, равное произведению
длины вектора
или на ось и называется число, равное произведению
длины вектора ![]() на косинус угла между этими векторами (между вектором
на косинус угла между этими векторами (между вектором ![]() и осью и)
и осью и)
![]()
В
ДПСК координаты вектора совпадают с проекциями вектора
![]()
![]() ,
,
![]() .
.
Поэтому
разложение вектора ![]() по базису
по базису ![]() будет иметь вид
будет иметь вид
![]()
или
![]()
или
![]()
Операции
сложения и умножения вектора на число, когда векторы заданы координатами,
сводятся к соответствующим операциям над их координатами
![]() ,
,
![]()
![]() .
.
Справедливость
последних выражений вытекает из
определений указанных операций и их свойств.
П р и м е р. Найдите сумму векторов ![]() и
и ![]() .
.
Р е ш е н и е.
![]()
![]() .
.
Векторы
![]() и
и ![]() коллинеарны, если их
координаты пропорциональны
коллинеарны, если их
координаты пропорциональны
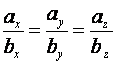
Векторы
![]() компланарны, если
выполняется условие
компланарны, если
выполняется условие
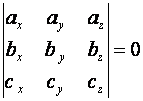 .
.
3.4. Скалярное произведение векторов
О п р е д е л е н и е. Скалярным произведением векторов ![]() и
и ![]() называется число,
равное произведению длин этих векторов на косинус угла между ними
называется число,
равное произведению длин этих векторов на косинус угла между ними ![]() .
.
Скалярное
произведение символически обозначается
![]() .
(4)
.
(4)
Если
воспользоваться определением, то скалярное произведение можно представить в
виде
![]() .
(5)
.
(5)
С в о й с т в а скалярного
произведения
1.
![]() =0, если
=0, если ![]()
2.
![]() , множители можно менять местами.
, множители можно менять местами.
3.
![]()
4.
![]()
В ы ч и с л е н и е скалярного произведения в ДПСК. Пусть векторы заданы координатами
![]() ,
,
![]() .
.
Учитывая свойства скалярного произведения, получаем
![]()
![]()
![]()
![]() .
.
С
учетом того, что
![]()
![]() ,
,
получается
![]() .
(7)
.
(7)
В частности
![]() ,
,
откуда
![]() . (8)
. (8)
Как
следует из выражения (4), скалярное произведение равно сумме произведений
соответствующих координат. С помощью выражений (5) и (6) получаем
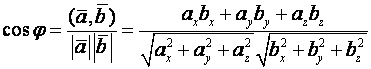 .
(9)
.
(9)
П р и м е р. Найдите скалярное произведение векторов ![]() и косинус угла между
ними.
и косинус угла между
ними.
Р е ш е н и е. Подставляем координаты векторов в формулу (4) и получаем значение
скалярного произведения
![]()
С помощью формулы (9)
находим косинус угла между векторами
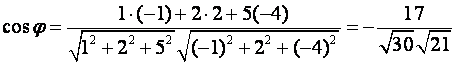 .
.
3.5 Векторное произведение векторов
О п р е д е л е н и е. Векторным произведением ![]() и
и ![]() называется вектор
называется вектор ![]() , удовлетворяющий следующим условиям
, удовлетворяющий следующим условиям
1.
![]() .
.
2.
![]() .
.
3.
Векторы ![]() образуют правую тройку
векторов.
образуют правую тройку
векторов.
Векторное
произведение символически обозначается
![]() .
.
Свойства
векторного произведения
1.
![]() ,
,
2.
![]() ,
,
3.
![]()
4.
Векторное
произведение по абсолютной величине равно площади параллелограмма, построенного
на этих векторах как на составляющих ![]()

![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вычисление
векторного произведения в ДПСК. Пусть
векторы заданы координатами
![]() ,
,
![]() .
.
Учитывая свойства векторного произведения, получаем
![]()
![]()
![]()
![]() .
.
С
учетом того, что
![]()
![]() ,
,
получаем
![]()
![]() (10)
(10)
или
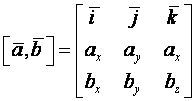 .
(11)
.
(11)
Векторное произведение в ДПСК согласно формуле (11)
представляет собой символический определитель третьего порядка. Элементы первой
строки – единичные векторы, элементы второй строки – координаты первого
вектора, элементы третьей строки – координаты второго вектора.
3.6.Смешанное произведение
О п р е д е л е н и е. Смешанным произведением трех векторов ![]() называется число,
которое получается, если векторы
называется число,
которое получается, если векторы ![]() и
и ![]() перемножить векторно и
затем полученный вектор перемножить с вектором
перемножить векторно и
затем полученный вектор перемножить с вектором ![]() скалярно.
скалярно.
Геометрический смысл смешанного произведения.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, 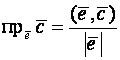 ,
,
![]() . (12)
. (12)
Если
![]() образуют правую тройку
векторов, то смешанное произведение
образуют правую тройку
векторов, то смешанное произведение ![]() , если левую, то
, если левую, то ![]() . Выражение (1) определяет объем параллелепипеда через векторы,
на которых он построен как на составляющих. Значит,
. Выражение (1) определяет объем параллелепипеда через векторы,
на которых он построен как на составляющих. Значит, ![]() . Поэтому смешанное произведение указывают без указания
знаков
. Поэтому смешанное произведение указывают без указания
знаков
![]() .
(13)
.
(13)
Вычисление смешанного произведения в декартовых системах. Векторное произведение
![]() .
.
умножим
на вектор ![]() скалярно
скалярно
![]() . (14)
. (14)
Раскроем определитель по элементам
третьей строки
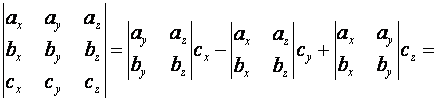
![]() . (15)
. (15)
Сравнивая
правые части равенств (14) и (15), получаем
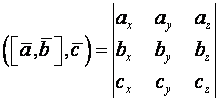 .
(16)
.
(16)
П р и м е р. Найдите объём и высоту параллелепипеда, построенного
на векторах
![]() , если A(1;2;3), B(2;1;4), D(4;1;5),
, если A(1;2;3), B(2;1;4), D(4;1;5), ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() D С
D С
![]()
![]() B
B
Р е ш е н и е. Введём обозначения ![]()
![]() . Подставляем
координаты векторов
. Подставляем
координаты векторов ![]() в формулу (16)
в формулу (16)
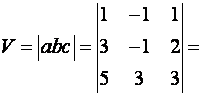
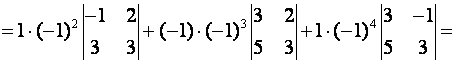
![]()
![]() .
.
Как известно, ![]() , откуда
, откуда
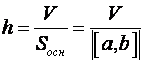 .
(17)
.
(17)
Находим ![]() . Для этого вычисляем векторное произведение
. Для этого вычисляем векторное произведение
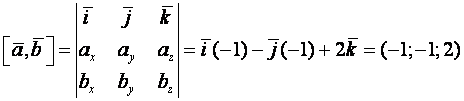 ,
,
находим
модуль полученного вектора ![]() . Подставляем значения
. Подставляем значения
![]() и
и ![]() в формулу (17) и получаем значение высоты
в формулу (17) и получаем значение высоты
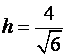 .
.
3.7. Системы координат
Помимо
ДПСК используются другие системы, а именно:
1.
Полярная
система координат
М

![]() О U
О U
![]() .
.
Связь между полярными и
декартовыми координатами можно получить, если луч OU совместить с ОХ, тогда ![]()
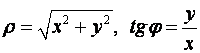 ,
, 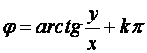 , где
, где ![]() при
при ![]() ,
,
![]() при
при ![]() ,
,![]() при
при ![]() .
.
Если же ![]() , то
, то
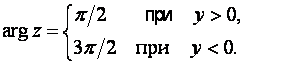
2)Цилиндрическая cистема координат (получается путем дополнения к полярным координатам координаты
аппликат).
ХУ
остается постоянным, добавляется Z.
![]() Z
Z
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() y Y
y Y
![]()
X
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
3) Сферическая система координат
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() .
.
Связь
сферических координат с декартовыми
![]()
Координатная
поверхность представляет собой сферу.