ЛЕКЦИЯ 4

 

 

2.6. Системы линейных алгебраических уравнений (СЛАУ)

 

 

Рассмотрим систему линейных алгебраических уравнений (СЛАУ)

    

                                                                     (1)

    Система (1) называется однородной, если свободные члены равны нулю  Однородная система всегда является совместной - она имеет решение  (возможно, не единственное).

Введём следующие обозначения

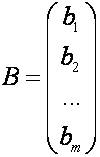,  ,  ,   .      (2)

         

Матрица  называется матрицей коэффициентов уравнения (1), матрица  называется расширенной матрицей  уравнения (1),  матрица  (матрица-столбец) называется столбцом неизвестных, матрица-столбец  называется столбцом свободных членов уравнения (1).

     Систему (1) с помощью матриц (2) можно представить в виде

.                                                           (3)

      Справедливость равенства (3) можно проверить путём непосредственной подстановки значений матриц    в это выражение

 ,

   то есть

 .                                    (4)

Выражение (4) представляет собой равенство двух матриц размером . Такие матрицы называют также матрицами-столбцами, так как они состоят из одного столбца. Приравнивая соответствующие элементы этих матриц, получаем систему линейных алгебраических уравнений (1).

Выражение (3) называется матричной  формой записи системы (1).

Рассмотрим отдельно случай квадратной системы, когда  и общий случай при .

 

2.6.1. Квадратная система

Существует три основных метода решения совместной СЛАУ

а) правило Крамера;

б) матричный способ;

в) метод Гаусса.

а) П р а в и л о Крамера. Пусть задана система

                                 (5)

Обозначим

 

      

 

.

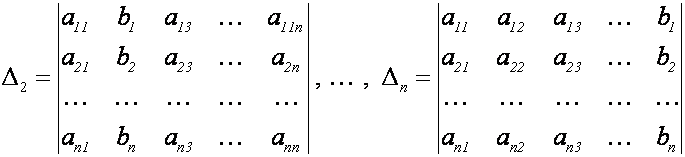Определитель  получается из определителя D заменой i-го столбца на столбец свободных членов. Правило Крамера состоит в том, что при неизвестные находятся с помощью формул:

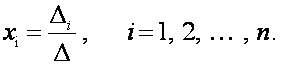                                              (6)

б) Матричный способ. Умножим равенство (5) слева на матрицу .

 

.                                                           (7)

Будем считать, что . В этом случае  существует. Теперь воспользуемся равенствами   и   , которые позволяют преобразовать выражение (7) к виду

.                                                             (8)

Выражение (8) представляет собой решение системы (1) в матричной форме. В этом и состоит матричный способ решения системы (5).

в) М е т о д Г а у с с а. При решении методом Гаусса расширенную матрицу  системы (5) элементарными преобразованиями приводят к трапецеидальному виду.

П р и м е р . Решите систему

 

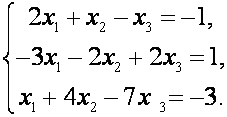
а) по правилу Крамера;

б) матричным способом;

в) методом Гаусса.

Р е ш е н и е. а) Правило Крамера.  Вычисляем определители

 

 

 

,  

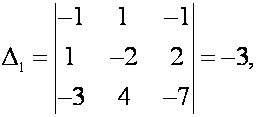
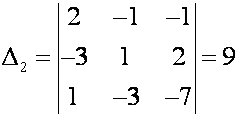Отсюда находимнеизвестные

 

 

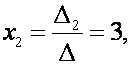
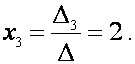
б) Матричный способ. Составляем матрицу коэффициентов и столбец свободных членов

 

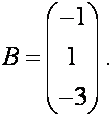
Теперь найдем  то обратная матрица существует. Находим алгебраические дополнения

        ;

            ;

   

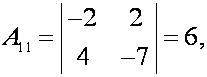
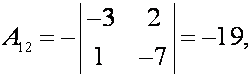
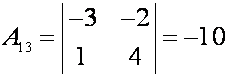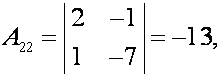
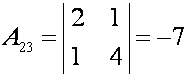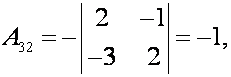
Составляем обратную матрицу

.

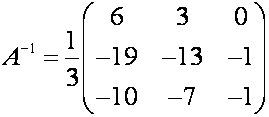И находим решение системы, для чего подставляем   и    в выражение (7)

.

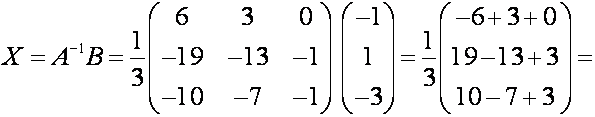
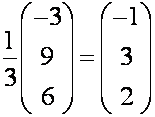Итак,

в) Метод Гаусса. Приводим расширенную матрицу  к трапе

 

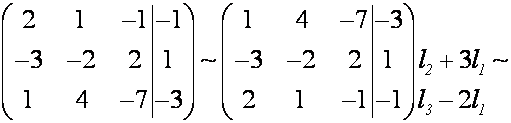
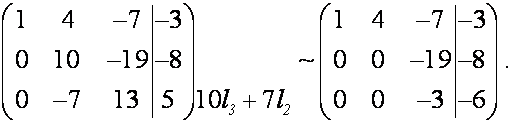
Последней матрице, имеющей треугольный вид (если исключить столбец свободных членов), соответствует следующая СЛАУ, равносильная исходной системе:

Из последнего уравнения находим , подставив его во второе уравнение, найдем  и, наконец, подставив найденные  и  в первое уравнение,  найдем :

       

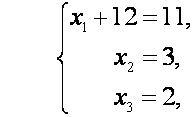
Следует иметь в виду, что при решении СЛАУ методом Гаусса перестановка столбцов приводит к перенумерации неизвестных.

2. Общий случай.

Теорема 3 (Кронекер–Капелли). Система (3) совместна в том и только в том случае, если ранг матрицы A равен рангу расширенной матрицы .

Систему (3) удобно решать методом Гаусса, который состоит в приведении расширенной матрицы  к трапецеидальному виду путем применения элементарных преобразований. Если при этом на некотором этапе получается строка, в которой все элементы, кроме элемента столбца свободных членов, равны нулю, то система несовместна. Если , то система (3) имеет бесчисленное множество решений, и каждое решение зависит от (n-r) не зависящих друг от друга параметров, т.е. степень свободы системы равна (n-r). В качестве параметров удобно брать «лишние неизвестные», которые объявляются свободными.

       Пример 8. Решить системы уравнений:                    

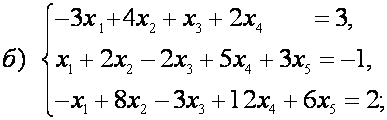
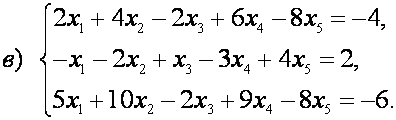
       Решение. Во всех трех системах воспользуемся методом Гаусса.

~

~.

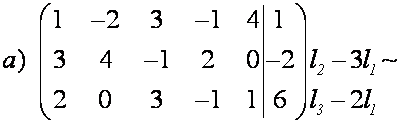
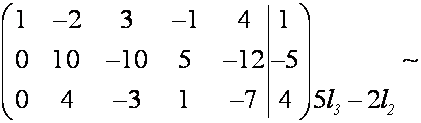
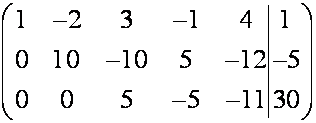Расширенная матрица приведена к трапецеидальному виду. Объявляем «лишние неизвестные» и свободными; запишем систему, соответствующую этой трапецеидальной матрице, перенеся свободные неизвестные и в правую часть:

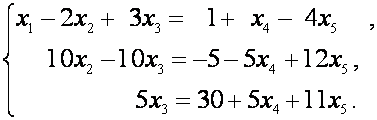
Степень свободы системы равна двум, значит решение системы выразится через два параметра. Положив  и решив систему из трех уравнений с неизвестными  найдем

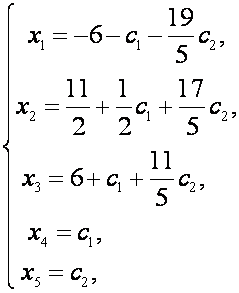
где  произвольные числа.

б)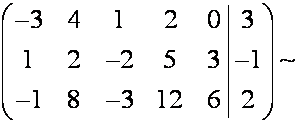

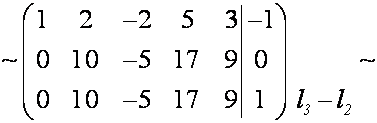
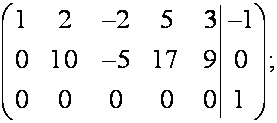
в результате преобразований появилась строка  следовательно, система несовместна.

в)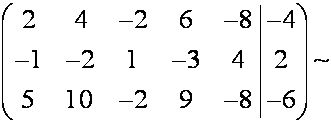

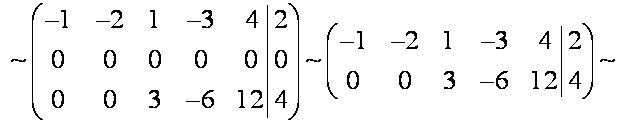
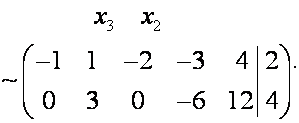
Ранг трапецеидальной матрицы равен 2, значит степень свободы равна  Объявляем неизвестные   свободными.

Положив  получим

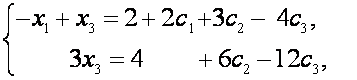
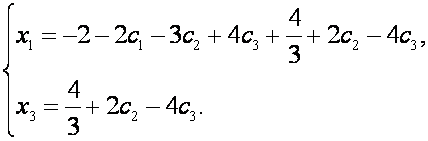
Таким образом, решением системы является

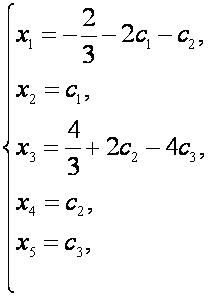
где произвольные числа (параметры).

Найдём решение этой системы. Для этого умножим равенство (3) слева на матрицу .

 

.                                                           (5)

Матрица   – это матрица, обратная к матрице . Будем считать, что . В этом случае  существует. Теперь воспользуемся равенствами   и   , которые позволяют преобразовать выражение (5) к виду

.                                                             (6)

Выражение (6) представляет собой решение системы (1) в матричной форме.

   П р и м е р. Найдите  решение системы

   Составляем матрицу коэффициентов и матрицу-столбец свободных членов заданной системы

,   .

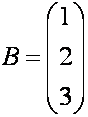   Находим обратную матрицу

.

Подставляем найденное значение обратной матрицы в выражение (6)

.

 

Итак, мы получили равенство

,

Откуда следует, что .

Замечание: если главный определитель системы равен 0, то нужно выделить уравнения, для которых определитель не равен 0, а свободные переменные переносятся в правую часть.