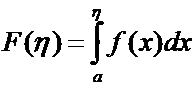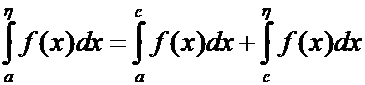ЛЕКЦИЯ 30
§10.11. Несобственные интегралы
10.11.1. Определение несобственных интегралов
О п р е д е л е н и е. Пусть
функция ![]() определена на конечном или бесконечном
полуинтервале
определена на конечном или бесконечном
полуинтервале ![]() ,
, ![]() и
интегрируема по Риману на любом отрезке
и
интегрируема по Риману на любом отрезке ![]() ,
, ![]() .
.
Функция переменного верхнего предела интегрирования
|
|
|
называется несобственным интегралом.
Если
предел 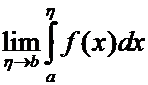 существует и конечен, то несобственный
интеграл называется сходящимся (существует),
существует и конечен, то несобственный
интеграл называется сходящимся (существует),
в противном случае, т.е. если этот предел равен бесконечности или не существует,
то несобственный интеграл называется расходящимся (не существует).
По определению,
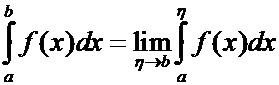 . (1)
. (1)
Возможны два случая:
1)![]() – конечно, т.е.
– конечно, т.е. ![]() ,2)
,2)
![]() .
.
Если ![]() и
и ![]() определена
на
определена
на ![]() и существует предел
и существует предел ![]() , который сходится, то в результате
получается интеграл Римана. Значит, интеграл Римана является частным случаем
несобственного интеграла и называется также собственным интегралом.
, который сходится, то в результате
получается интеграл Римана. Значит, интеграл Римана является частным случаем
несобственного интеграла и называется также собственным интегралом.
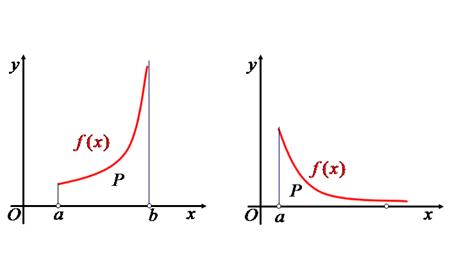
Геометрический
смысл несобственного и собственного интегралов идентичны, т. е. несобственный
интеграл от неотрицательной функции ![]() равен площади криволинейной
трапеции
равен площади криволинейной
трапеции
![]() ,
,
образованной
графиком функции ![]() . Причём эта трапеция как в
первом случае, когда функция
. Причём эта трапеция как в
первом случае, когда функция ![]() неограниченная, а
промежуток
неограниченная, а
промежуток ![]() конечный, так и во втором случае, когда
функция
конечный, так и во втором случае, когда
функция ![]() ограниченная, а промежуток
ограниченная, а промежуток ![]() бесконечный, всегда является
неограниченным множеством
бесконечный, всегда является
неограниченным множеством
Если
![]() , то
, то
|
|
|
В этом случае несобственный интеграл (1) существует только тогда, когда существует несобственный интеграл
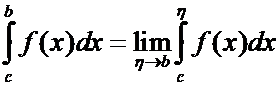 (2)
(2)
и наоборот. Итак, в случае существования интегралов (1) и (2) имеем
|
|
(3)
|
Интегралы
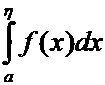 и
и 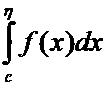 в
равенстве (3) – несобственные, а интеграл
в
равенстве (3) – несобственные, а интеграл 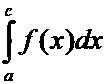 –
собственный.
–
собственный.
Если
функция ![]() определена на полуинтервале
определена на полуинтервале ![]() ,
, ![]()
и
интегрируема по Риману на любом отрезке ![]() ,
, ![]() , то несобственный интеграл
, то несобственный интеграл
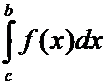
определяется как функция
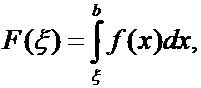
представляющая собой интеграл с переменным нижним пределом интегрирования.
Выражение (1) в этом случае будет иметь вид
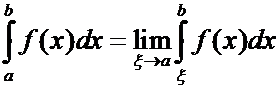 .
(4)
.
(4)
З а м е ч а н и е. Несобственные интегралы от неограниченных функций по конечному промежутку называются также несобственными интегралами второго рода (типа),
а несобственные интегралы от ограниченных функций по бесконечному промежутку
называются также несобственными интегралами первого рода (типа).
10.10.2. Свойства несобственного интеграла
Свойства несобственного интеграла аналогичны свойствам определенного интеграла.
1°.
(Формула Ньютона ![]() Лейбница). Если
Лейбница). Если ![]()
![]() какая-либо
первообразная функции
какая-либо
первообразная функции ![]() на полуинтервале
на полуинтервале ![]() , то
, то 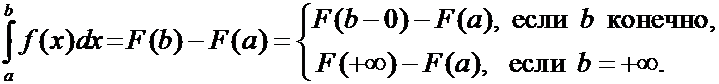 (1)
(1)
Это равенство понимается в том смысле, что либо обе его части одновременно имеют смысл, и тогда они равны, либо они одновременно не имеют смысла, т. е. стоящие в них пределы не существуют.
Согласно
формуле Ньютона-Лейбница для функций, интегрируемых по Риману, для любого ![]() имеем
имеем
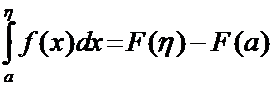 .
.
Перейдя
в этом равенстве к пределу при ![]() , получим формулу (1).
, получим формулу (1).
2°.
(Линейность). Если несобственные интегралы 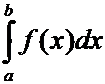 и
и 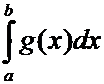 сходятся, то для любых чисел
сходятся, то для любых чисел ![]() ,
, ![]() сходится
и несобственный интеграл
сходится
и несобственный интеграл 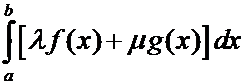 , причём
, причём
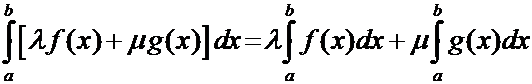 .
.
3°.(Интегрирование
неравенств). Если интегралы 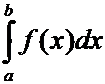 и
и 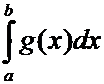 сходятся и для всех
сходятся и для всех ![]() выполняется неравенство
выполняется неравенство ![]() , то
, то
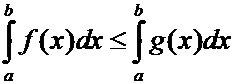 .
.
4°.(Правило
интегрирования по частям). Если функции ![]() и
и ![]() кусочно
кусочно ![]() непрерывно
дифференцируемы на каждом отрезке
непрерывно
дифференцируемы на каждом отрезке ![]() ,
, ![]() , то
, то
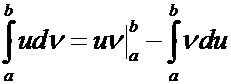 ,
,
причём
если любые два из выражений 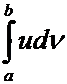 ,
, ![]() и
и 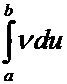 имеют
смысл (т.е. соответствующие пределы конечны), то имеет смысл и третье.
имеют
смысл (т.е. соответствующие пределы конечны), то имеет смысл и третье.
5°.(Замена переменной). Пусть
функция ![]() непрерывна на
непрерывна на ![]() ,
функция
,
функция ![]() непрерывно дифференцируема на
полуинтервале
непрерывно дифференцируема на
полуинтервале ![]() ,
, ![]() ,
причём
,
причём ![]() при
при ![]() ; тогда
; тогда
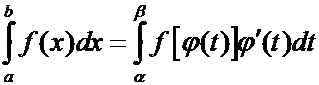 .
.
З а м е ч а н и е. Если
функция ![]() определена на
определена на ![]() , то
, то
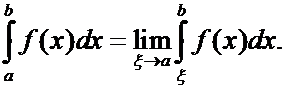
З а м е ч а н и е.
Несобственный
интеграл 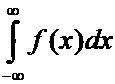 представляется в виде
суммы двух интегралов
представляется в виде
суммы двух интегралов
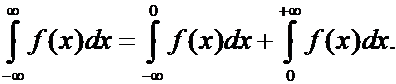
Интеграл
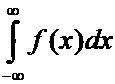 сходится, если сходятся интегралы
сходится, если сходятся интегралы
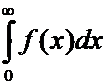 и
и 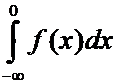 . Однако
могут быть случаи, когда каждый из интегралов
. Однако
могут быть случаи, когда каждый из интегралов 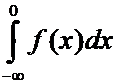 и
и 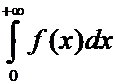 расходится, но интеграл
расходится, но интеграл

сходится.
В этом случае говорят, что 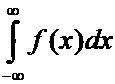 сходится в смысле
главного значения Коши
сходится в смысле
главного значения Коши
и записывается это так
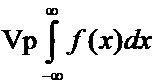 .
.
Аналогично
и для несобственного интеграла второго рода определяется главное значение интеграла
в смысле Коши, т. е. если функция![]() не ограничена в точке
не ограничена в точке ![]() ,
, ![]() , то
, то
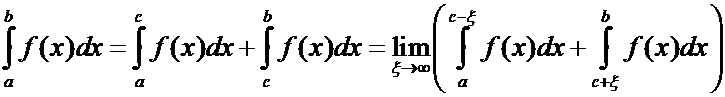 .
.
Если предел конечный, то полагают
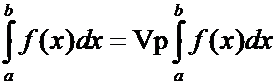 .
.
Иногда достаточно установить сходится или расходится несобственный интеграл, не вычисляя этого интеграла.
С этой целью используются признаки сравнения.
Т е о р е м а 1.(Первый
признак сравнения). Пусть ![]() ,
тогда
,
тогда
если
интеграл 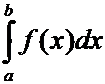 сходится, то сходится и интеграл
сходится, то сходится и интеграл 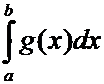 ;
;
если
интеграл 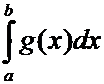 расходится, то расходится и интеграл
расходится, то расходится и интеграл 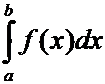 . (Без док.)
. (Без док.)
Т е о р е м а 2(Второй
признак сравнения). Пусть ![]() и
и ![]() на
на ![]() , при
этом
, при
этом 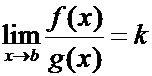 ,
, ![]() ,
тогда
,
тогда 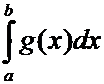 и
и 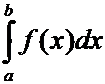 сходятся
или расходятся одновременно. (Без док.)
сходятся
или расходятся одновременно. (Без док.)
З а м е ч а н и е. При
применении признаков сравнения в качестве вспомогательной функции ![]() часто используются функции вида
часто используются функции вида
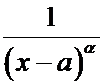 ,
, 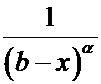 ,
, ![]() .
.
Несобственные
интегралы от этих функции при ![]() сходятся.
сходятся.