ЛЕКЦИЯ 3
2.
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
2.1. Понятие
матрицы
О п р е д е л е н и е. Матрицей называется прямоугольная таблица чисел,
состоящая из m строк и n столбцов. ![]() – порядок или размер матрицы. Например, матрица
– порядок или размер матрицы. Например, матрица
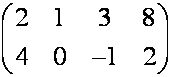
имеет
размер ![]() , так как в этой
матрице количество строк равно
, так как в этой
матрице количество строк равно ![]() , а количество столбцов равно
, а количество столбцов равно ![]() . Числа, из которых состоит матрица, называются элементами. В
общем случае матрицы символически обозначаются следующим образом
. Числа, из которых состоит матрица, называются элементами. В
общем случае матрицы символически обозначаются следующим образом
 .
.
Типы
матриц:
1.
Прямоугольные – ![]() .
.
2.
Квадратные – ![]() .
.
3.
Трапецеидальные –
прямоугольные матрицы, у которых ![]() при
при ![]() или
или ![]() .
.
4.
Треугольные –
квадратные матрицы, у которых ![]() при
при ![]() или
или ![]() .
.
5.
Диагональные –
квадратные матрицы, у которых ![]() при
при ![]() .
.
6.
Единичная
матрица – диагональная
матрица, у которой ![]() .
.
7.
Траспонированная
матрица ![]() – это матрица, которая получается из матрицы
– это матрица, которая получается из матрицы ![]() путём замены в ней строк столбцами.
путём замены в ней строк столбцами.
П р и м е р ы
м а т р и ц.
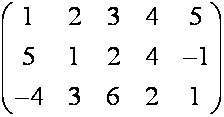 –
прямоугольная матрица,
–
прямоугольная матрица,
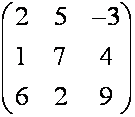 –
квадратная матрица,
–
квадратная матрица,
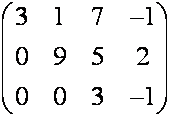 – трапецеидальная матрица,
– трапецеидальная матрица,
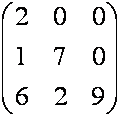 –
треугольная матрица,
–
треугольная матрица,
 – диагональная матрица,
– диагональная матрица,
 – единичная матрица.
– единичная матрица.
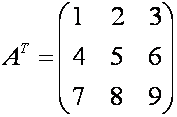 – транспонировання матрица для матрицы
– транспонировання матрица для матрицы 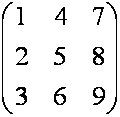
2.2. Действия с матрицами
С матрицами можно выполнять следующие операции:
1)
Сложение матриц. Матрица ![]() называется суммой
матриц
называется суммой
матриц ![]() , если
, если ![]() , Матрица А и В
должны быть одного и того же порядка, Матрица С получится того же порядка, что и матрицы А и В.
, Матрица А и В
должны быть одного и того же порядка, Матрица С получится того же порядка, что и матрицы А и В.
П р и м е р. Найдите сумму матриц 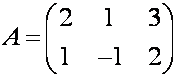 и
и 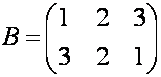 .
.
Р е ш е н и е. Элементы матрицы
![]() получаем путём
суммирования соответствующих элементов матриц
А и В
получаем путём
суммирования соответствующих элементов матриц
А и В
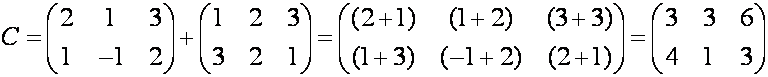
2) Умножение
матрицы на число. Матрица ![]() называется
произведением матрицы
называется
произведением матрицы ![]() на число
на число ![]() если
если ![]() .
.
П р и м е р.
Найдите произведение матрицы 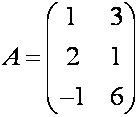 на число
на число ![]() .
.
Р е ш е н и е. Элементы матрицы ![]() получаем путём
умножения элементов матрицы
получаем путём
умножения элементов матрицы ![]() на число
на число ![]()
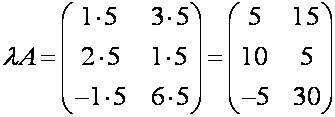
3) Умножение
матриц. Матрица ![]() называется
произведением матрицы
называется
произведением матрицы ![]() размером
размером ![]() и матрицы
и матрицы ![]() размером
размером ![]() , если элементы матрицы
, если элементы матрицы
![]() вычисляются по
формуле
вычисляются по
формуле
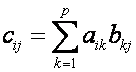 (1)
(1)
Перемножать
можно только матрицы, у которых количество столбцов первой равно количеству
строк второй. Произвольные матрицы перемножать нельзя.
П р и м е р. Найдите произведение матриц
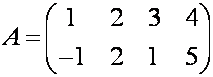 и
и 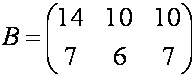 .
.
Р е ш е н и е. Согласно формуле
(1), имеем
![]()
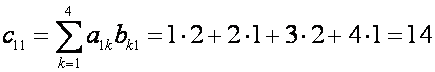 ,
,
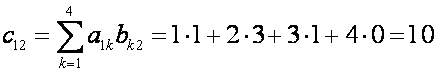 ,
,
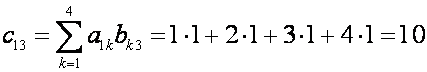 ,
,
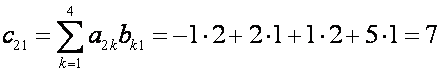 ,
,
 ,
,
 .
.
Значит,
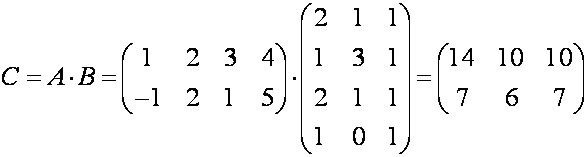 .
.
Рассмотренные
операции с матрицами обладают теми же свойствами, что и операции
сложения и умножения для вещественных чисел, за исключением произведения
матриц, которое не коммутативно, т.е. ![]() . В этом можно убедиться с помощью следующего примера для
матриц
. В этом можно убедиться с помощью следующего примера для
матриц 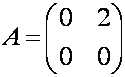 и
и 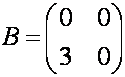 . Находим произведения
. Находим произведения
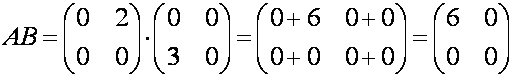 ,
,
 .
.
Как
видим, 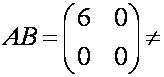
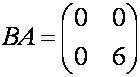 .
.
2.3. Определители
Каждой квадратной матрице по определённому правилу
можно поставить в соответствие единственное число. Это число называется определителем и
символически обозначается
 .
.
Порядок определителя равен порядку квадратной матрицы.
Определитель
второго порядка вычисляется следующим образом
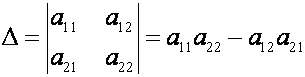 ,
(2)
,
(2)
т.е. из произведения элементов, стоящих на так
называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний
угол), вычитается произведение элементов, находящихся на побочной диагонали (идущей из левого нижнего
в правый верхний угол).
П р и м е р. Вычислите определитель матрицы 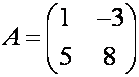 .
.
Р
е ш е н и е. Значения элементов
матрицы ![]() , т.е.
, т.е.
![]()
Подставляем
в формулу (2) и получаем
![]() .
.
Определитель
третьего порядка вычисляется с помощью формулы

![]() (3)
(3)
З а м е ч а н и е. Чтобы легче
запомнить эту формулу, можно использовать так называемое правило треугольников
(правило Саррюса). Оно заключается в следующем. Элементы, произведения которых входят
в определитель со знаком «+», располагаются на главной диагонали и в вершинах
треугольников, симметричных относительно
главной диагонали
![]()
![]()
![]()

![]()
![]()

![]()

Элементы,
произведения которых входят в определитель со знаком «–», располагаются
аналогичным образом относительно побочной диагонали
![]()
![]()

![]()
![]()



![]() П р и м е р. Вычислите определитель матрицы
П р и м е р. Вычислите определитель матрицы 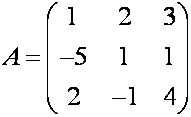 .
.
Р е ш е н и е. Подставляем значения элементов матрицы в формулу (3) и находим
величину заданного определителя
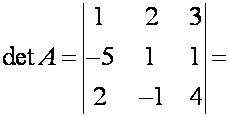
![]()
![]()
Для вычисления определителей третьего
порядка можно пользоваться ещё правилом «3![]() 5». Согласно этому правилу к заданной матрице
5». Согласно этому правилу к заданной матрице

добавляют
ещё первые два столбца
![]()
 .
.
Элементы, произведения которых входят в определитель
со знаком «+», располагаются на главной диагонали и на отрезках, параллельных
главной диагонали



![]()
 .
.
Элементы, произведения которых входят в определитель
со знаком «–», располагаются на побочной диагонали и на отрезках, параллельных
побочной диагонали



![]()
 .
.
Определитель
![]() равен сумме указанных
произведений элементов с учетом их
знаков.
равен сумме указанных
произведений элементов с учетом их
знаков.
Основные
свойства определителей
Рассмотрим основные свойства определителей 2-го и 3-го
порядка
С в о й с т в о
1. Определитель не
изменяется при транспонировании, т.е.
![]() .
(4)
.
(4)
Действительно,

![]() ,
,

=![]() ,
,
Из чего следует
справедливость равенства (4).
Из свойства 1
следует, что свойствами определителей,
сформулированные для строк будут такими же как и для столбцов. Поэтому следующие свойства определителей будут формулироваться
только для строк.
С в о й с т в о 2. При умножении элементов строки определителя на
некоторое число определитель умножается
на это число, т.е.
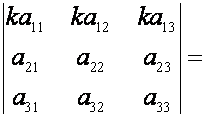

В справедливости этого свойства можно убедиться,
вычислив эти определители
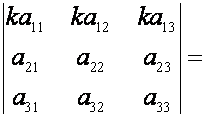
![]()
![]()
![]()

Свойство 3.
Определитель равен нулю в следующих
случаях:
a)
одна из строк
нулевая
 ,
,
б) две равные строки

в) элементы
двух строк пропорциональны
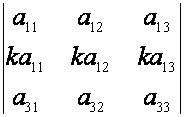
В
справедливости перечисленных свойств легко убедиться с помощью формулы (3).
С в о й с т в о 4. Если две какие-либо строки определителя поменять
местами, то знак определителя изменится на противоположный


Доказательство
этого свойства выполняется с помощью формулы (3).
С в о й с т в о
5. Если в
определителе некоторая строка, например, первая является линейной
комбинацией двух строк с коэффициентами ![]() и
и ![]()
![]() ,
,
то определитель будет
равен сумме двух определителей, определяемых формулой
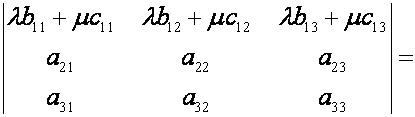
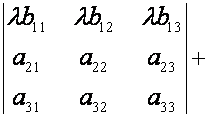
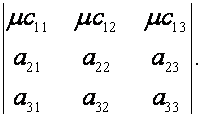
Справедливость
этого свойства можно доказать, сравнив значения левой и правой частей
равенства, найденные с помощью формулы (3).
С в о й с т в о
6. Величина определителя
не изменится, если к элементам одной строки прибавить соответствующие элементы
другой строки, умноженные на одно и то же число
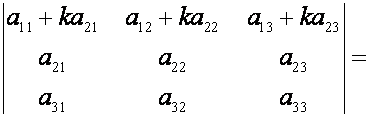

2.4. Обратная матрица
Минором ![]() к элементу
к элементу ![]() матрицы
матрицы ![]()
![]() -го порядка называется определитель
-го порядка называется определитель ![]() -го порядка той матрицы, которая получается из матрицы
-го порядка той матрицы, которая получается из матрицы ![]() в результате
вычёркивания
в результате
вычёркивания ![]() -ой строки и
-ой строки и ![]() -го столбца.
-го столбца.
О п р е д е л е н и е. Матрица В
называется обратной матрице А, если
АВ=ВА=Е.
Символически
обратная матрица обозначается ![]() . Вычисляется обратная матрица с помощью формулы
. Вычисляется обратная матрица с помощью формулы
|
|
(5) |
где ![]() – алгебраическое
дополнение к элементу
– алгебраическое
дополнение к элементу ![]() .
.
Вырожденной
матрицей называется матрица, у которой
определитель равен 0.
Обратные
матрицы могут иметь только невырожденные матрицы.
П р и м е р. Найти матрицу, обратную к
матрице 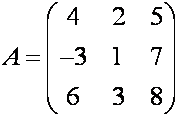 .
.
Р е ш е н и е. Вычисляем
определитель
![]() .
.
Так
как определитель матрицы не равен нулю, то ![]() существует. Найдем
алгебраические дополнения:
существует. Найдем
алгебраические дополнения:
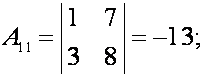
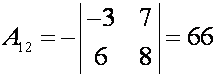 ;
; 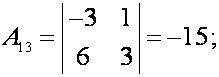
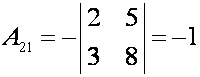 ;
; 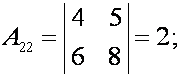
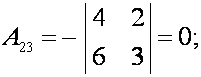
![]()
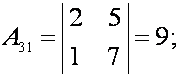
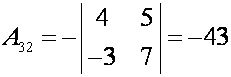 ;
; 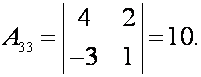
Подставляем
найденные значения определителя матрицы и алгебраических дополнений в формулу
(5) и получаем искомое значение обратной
матрицы
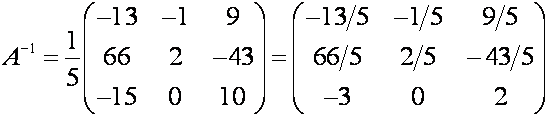 .
.
Выполним проверку, для чего вычислим
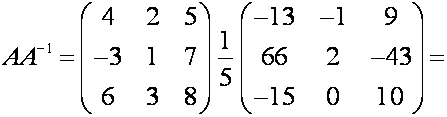
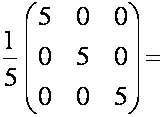

и
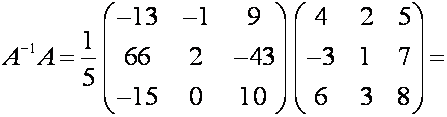


Как видим, оба произведения
равны единичной матрице. Значит, обратная матрица вычислена верно.
2.5 Ранг матрицы
Рангом
матрицы А называется число r,
удовлетворяющее следующим двум требованиям:
1.
Существует минор ![]() порядка r.
порядка r.
2.
Все миноры порядка
r+1 равны 0.
Наиболее
простой способ вычисления ранга матрицы сводится к приведению матрицы к
трапециидальному виду.
Пример:
Определить
ранг матрицы А.
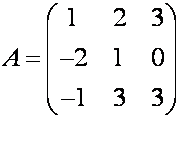 Домножаем первую строчку так, чтобы во второй и третьей
получились нули. В данном случае домножаем на 2 и 1
Домножаем первую строчку так, чтобы во второй и третьей
получились нули. В данном случае домножаем на 2 и 1
 Повторяем те же действия, только теперь вторую строчку
домножаем на (-1),чтобы в третьей
получились нули.
Повторяем те же действия, только теперь вторую строчку
домножаем на (-1),чтобы в третьей
получились нули.
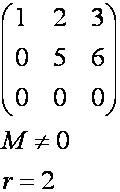
Теорема Кронекера-Капелли. Система линейных алгебраических уравнений имеет
решения (т.е. совместна)тогда и только тогда, когда ранг расширенной матрицы
равен рангу основной матрицы.
2.6. Матричный способ решения СЛАУ
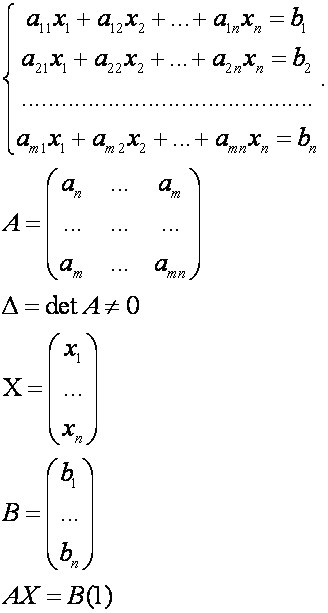
Выражение
(1)-матричная форма записи системы.
Так
как матрица А невырожденная, она имеет обратную матрицу ![]() . Умножим равенство
(1) слева на
. Умножим равенство
(1) слева на ![]()
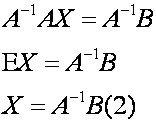
Выражение
(2) представляет собой решение в матричной форме.
Пример: решить систему.

Замечание:
если главный определитель системы равен 0, то нужно выделить уравнения, для
которых определитель не равен 0, а свободные переменные переносятся в правую
часть.
 ,
,